ADC 是将模拟信号转换为等效数字信号的设备。将模拟信号转换为分立时间信号的过程称为"采样",将其转换为离散振幅信号的过程称为"量化"。ADC 可转换的模拟电压的最大振幅称为ADC的"满量度输入电压"
在 N 位 ADC 中,满量分量分2^n水平。步进大小由 $\Delta = \frac{A}{2^N}$
其中 A 是最大输入范围。
步进尺寸是输入电压的最小变化,可由ADC解析。步进尺寸的概念与ADC的分辨率N密切相关。
例如,如果 N=3 有 8 级。
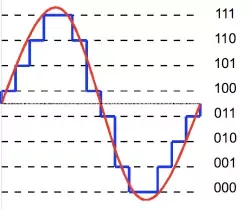
红色下弦波表示模拟输入,而蓝色曲线表示 8 级量化的内电波。与量化正弦波的每个级别关联的 3 位数是 ADC 的数字输出。如果输入范围为 1 V,则步进大小为 0.125 V。数字输出 000 对应于 0 V,111 对应于 0.875 V。
闪存ADC
有不同的技术来数字化模拟信号。例如,闪存ADC具有每个电平的电压参考和比较器。每个比较器都连接到输入和其中一个引用。模拟输入与所有引用同时进行比较。这允许在时钟的单个周期内确定最接近模拟输入值的电平。
斜坡ADC
另一种技术是将模拟输入与一个斜坡进行比较,其值从输入范围的最小值增大到最大值。由于根据设计,斜坡值是已知的时间函数,因此当斜坡达到与模拟输入相同的值时,将确定数字值。由于输入范围的所有值都需要与模拟输入进行比较,因此此 ADC 速度非常慢。
为了加快转换速度,只要斜坡值与输入电平相同,就可以停止斜坡。这将允许立即开始新的转换,如下图所示。
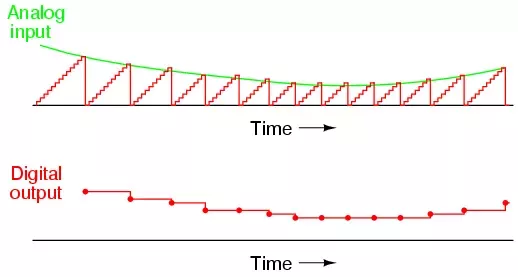
但是,此方法会导致输入的不均匀采样,这在大多数数字信号处理设计中是不能接受的。
SAR ADC
连续近似寄存器 (SAR) ADC 比斜坡 ADC 快得多,但仍比闪存ADC慢得多。SAR ADC 的转换时间至少需要时钟的 N 个周期来计算数字输出。N 位 SAR ADC 包括轨道和保持电路、比较器、N 位寄存器和一些逻辑。
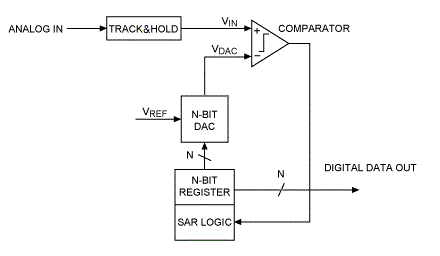
当斜坡ADC对输入范围的所有值执行详尽搜索时,SAR ADC 执行二进制搜索。SAR ADC 将模拟输入与输入范围的中间值进行比较。根据结果,新的搜索在输入范围的上半部分或下半部分执行。如果选择了下半部分,则模拟输入与输入范围的 1/4 进行比较,否则模拟输入与输入范围的 3/4 进行比较。每次迭代时,搜索范围都会减半。
通常,N 位 SAR ADC 需要 N 次迭代,因此需要 N 个时钟周期来计算数字输出。
例如,让我们考虑一个输入范围为 0 到 1 V 的 4 位 SAR ADC,假设模拟输入为 0.7 V。
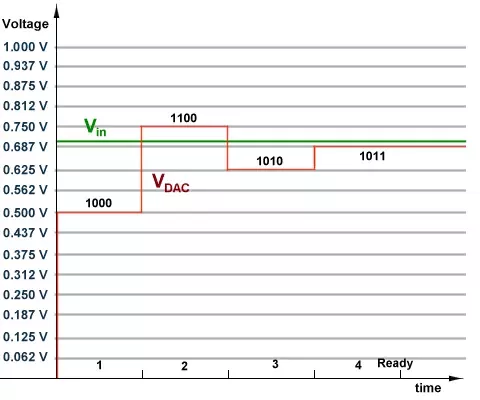
输入范围的中间值为0.5V。在第一次迭代中,将模拟输入0.7 V与0.5 V进行比较。由于0.7高于0.5,因此需要在输入范围的上半部分执行新的搜索。在第二次迭代中使用的值为0.750 V(0.5 + 0.5 1/2)。由于0.7小于0.750,因此第三次迭代的搜索值为0.625 V(0.750-0.25 1/2)。现在o.7 V高于0.625 V,因此对于第四次也是最后一次迭代,搜索值为0.6875 V(0.625 + 0.125 1/2)。0.6875 V对应于二进制数1011,它也是ADC的数字输出。
该算法的实现非常简单。
跟踪和保持的目的是确保比较器输入$V_{IN}$在转换过程中不会改变。该电路以采样率1对模拟输入进行采样$\frac{1}{f_s}$ 在很短的时间内跟踪它,然后保持其值直到下一次转换。
DAC将寄存器的内容转换为模拟信号。比较器将模拟输入与DAC输出进行比较。
根据比较器的结果,SAR算法一次从最高有效位开始一次处理一个寄存器的位,每个时钟周期一位。
在每次转换(第一次迭代)开始时,清除寄存器并将MSB设置为1。这将产生一个DAC输出,该输出等于输入范围的中间值(在本示例中为0.5 V)。如果模拟输入高于DAC输出,则在第二次迭代中,MSB保持不变,并将其旁边的位设置为1,否则将MSB设置为0,并将其旁边的位设置为1。重复该过程,直到处理完所有N位为止。
本回答来自Luciano Zoso, studied Electrical and Electronics Engineering at Polytechnic University of Turin
 理工酷
理工酷
 资源下载
资源下载