0
1.电网数学建模,首先需要对电网进行简化以及数学建模,电力系统的建模包括两大部分,分别是元件建模和网络建模,元件建模的对象包括同步发电机,电力负荷等,网络建模的对象则是线路,变压器等。电力系统建模时具有一些特点,例如线路,变压器在稳态运行条件下是线性且定常元件,研究电力系统暂态时,一般故障分析中稳态短路电流计算仍然是稳态分析
2.确定已知的负载和供电条件下,可以得到的信息,进行节点分析,已知的信息包括:线路阻抗,每个负载母线上的负载,发电机的参数等,节点分析的好处包括:数据准备简单,变量和方程的数量较少等。
3.总线或节点类型识别,潮流分析中总线共分为三类,发电机总线(PV总线),是已知电压幅度和注入的有功功率的总线,电压相角和注入的无功功率未知(待解);负载总线(PQ总线),已知注入的有功功率和无功功率,电压幅度和电压相角未知。最后是松弛总线(slack bus),是参考总线,所有其他总线的电压相位角均以它为基准(所以松弛总线的相位角一般为0),系统中只有一根。
4.稳态分析中,由于稀疏矩阵而使用的是节点导纳矩阵(Y总线矩阵)方法,导纳从定义上是阻抗的倒数,导纳矩阵的对角元素Yii等于节点i处所有的导纳的总和,而非对角元素Yik是节点i与k之间的分支导纳的相反数。(见下图)
5.潮流分析最后得到的方程通常没有封闭解,需要使用迭代方式来解决,通常有两种方法,分别是高斯-赛德尔法(Gauss–Seidel method)和牛顿-拉夫森法(Newton-Raphson method)
6.最后潮流分析可以获得每个总线的电压幅度和角度,每个发电机的有功和无功发电,每条线上的功率流和系统总损耗等。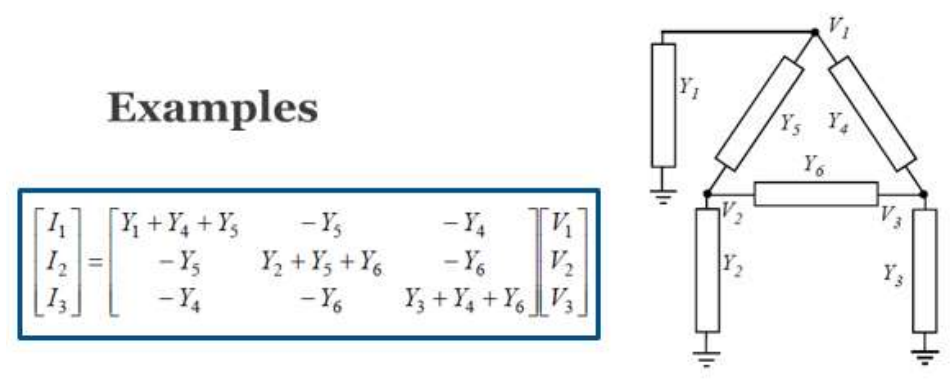
收藏
 理工酷
理工酷
 资源下载
资源下载