0
假设有一个具有1个隐藏层的神经网络。
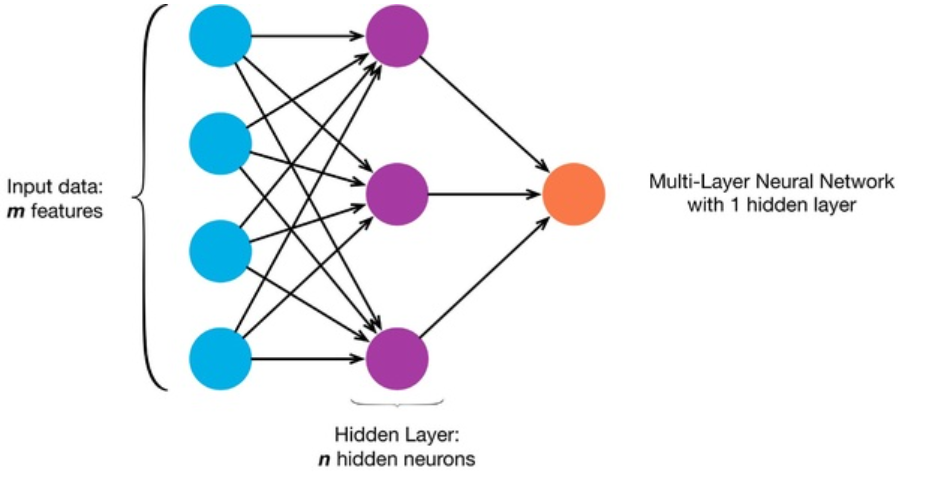 假设隐藏层中的每个节点都经过自定义的激活函
数“ a_h ”计算,
假设隐藏层中的每个节点都经过自定义的激活函
数“ a_h ”计算,
Z=Wh∗x+bh ah=sigmoid(Z) W_h是每次通过时要更新的隐藏层的权重。 x是来自先前输入层的输入。 b_h是隐藏层的偏差项。
现在,如果将所有节点的W和b初始化为零,则隐藏层的所有节点将具有相同的权重' W '和相同的偏差' b '。因此,它们将具有相同的激活“ a_h” 。
输出层将计算 yo=sigmoid(Wo∗ah+bo) 由于W_out和b_out也被初始化为零(根据问题), y_out将为sigmoid(0),等于0.5 。
这样就结束了向前传播。
在反向传播期间,我们从损失函数L开始计算dW ,db和da 。
涉及到一些演算,但是事实证明,对于隐藏层的所有3个节点,dW都是相同的,因为Z对于所有节点都是相同的。
因此,当你使用以下公式更新权重时,所有三个节点的W均相同。
W=W−(alpha∗dW) α是学习率。
因此,所有节点最终都将具有相同的值,与在隐藏层中只有一个节点没有什么不同。因此,你的网络最终只会学习一种功能,而神经网络的目标是让不同的节点计算不同的功能。这称为“对称性问题” 。
为了打破这种对称性,我们随机初始化权重。
收藏
 理工酷
理工酷
 资源下载
资源下载









