交叉熵通常用于量化两个概率分布之间的差异。通常,“真实”分布(机器学习算法试图匹配的分布)表示为单热分布。例如,假设对于一个特定的训练实例,真标签是B(在可能的标签A、B和C中)。因此,此训练实例的一个热分布是:
Pr(A类)Pr(B类)Pr(C类)
0.0 1.0 0.0
你可以将上述的真实分布解释为训练实例具有0%的A类概率、100%的B类概率和0%的C类概率。
现在,假设你的机器学习算法预测以下概率分布:
Pr(A类)Pr(B类)Pr(C类)
0.228 0.619 0.153
预测的分布与真实分布有多接近就是交叉熵损失所决定的。使用以下公式:
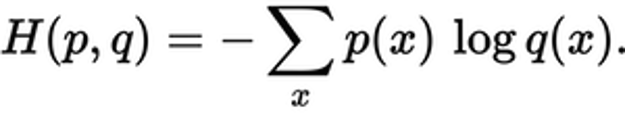
其中p(x)是真实概率分布,q(x)是预测概率分布。总和超过了A、B和C三个等级。在这种情况下,损失为0.479:
H=-(0.0*ln(0.228)+1.0*ln(0.619)+0.0*ln(0.153))=0.479
所以这就是你的预测与真实分布的“错误”或“遥远”的程度。
交叉熵是许多可能的损失函数中的一个(另一个流行的是SVM铰链损失)。这些损失函数通常写为J(θ),可以在梯度下降中使用,梯度下降是一种迭代算法,用于找到参数(或系数)的最佳值。在下面的等式中,用H(p,q)代替J(θ)。但请注意,首先需要计算H(p,q)对参数的导数。
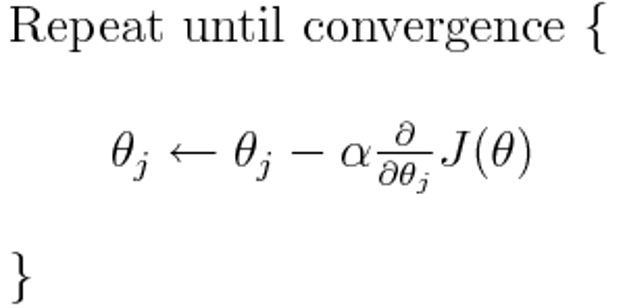
下面直接回答你的原始问题:
它只是描述损失函数的一种方法吗?
是的,交叉熵描述了两个概率分布之间的损失。它是许多可能的损失函数之一。
我们可以使用梯度下降算法来寻找最小值,梯度可以作为熵的交叉下降部分。
 理工酷
理工酷
 资源下载
资源下载