理工酷

如果要通俗地解释这个问题，你可以认为它等于一个随机选择的正例排名高于一个随机选择的反例的概率（被认为是正的概率高于反的概率）。 为简单起见，比如说有N个正面和N个负面例子。将所有2N个示例放在[0,1]上，该点等于分类器将该示例标记为正的概率。希望正面的例子大多在1附近。 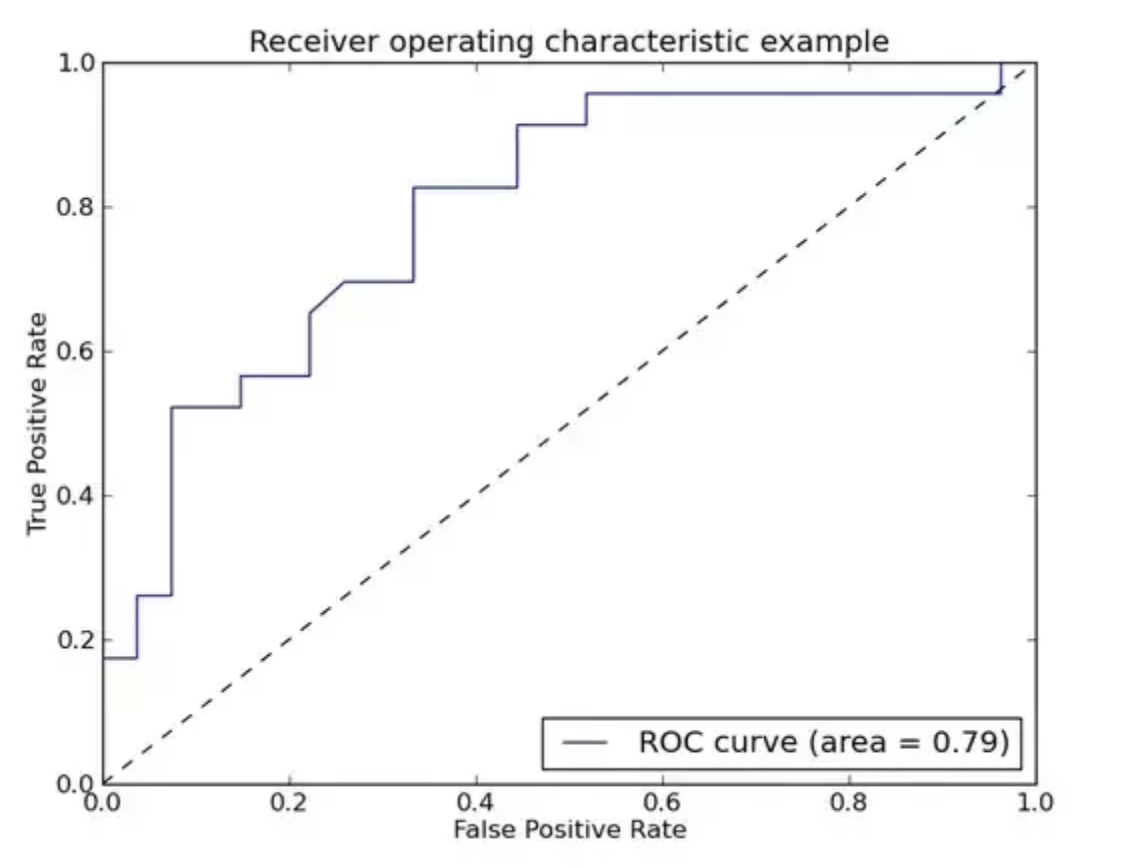当你将分类器的阈值从1移到0时，将有0%到100%的示例高于阈值。这些对应于ROC曲线的左下角点（0％真/假阳性率）和曲线的右上角点（100％真/假阳性率）。移动阈值就像绘制曲线。 如果以完整的“分辨率”绘制曲线，则曲线本身会在降低阈值时以大小为1 / N的阶梯步长移动。 （为简单起见，上表显示了一个关系，它产生一个“倾斜”的变化。） 它仅在阈值越过一个点时移动。如果它超过一个正点，那么真阳性率就会下降1 / N，因为它的计数减少了1，再除以示例总数N，曲线向下跳。同样，如果它越过否定示例，则假阳性率下降1 / N。曲线向左跳。 所以沿x轴的1/N的每一部分对应一个负例。现在选取概率为1/N的任何一个负例，想象一下当阈值接近那个负例时。高于它的阳性病例比例是该点的真阳性率。但这也是一个随机的正例在这一点之上的概率，因此，一个随机正样本超过随机负样本的总概率是所有负样本中TP总和的1 / N倍。但上述情况只是x轴的一点宽度为1 / N时，对应于每个负例，乘以该点的曲线高度TP再加起来，你也可以得到曲线的面积。