0
主成分分析(PCA)和线性判别分析(LDA)是两种常用的数据预处理线性变换技术,用于降维,以选择可用于最终机器学习算法的相关特征。
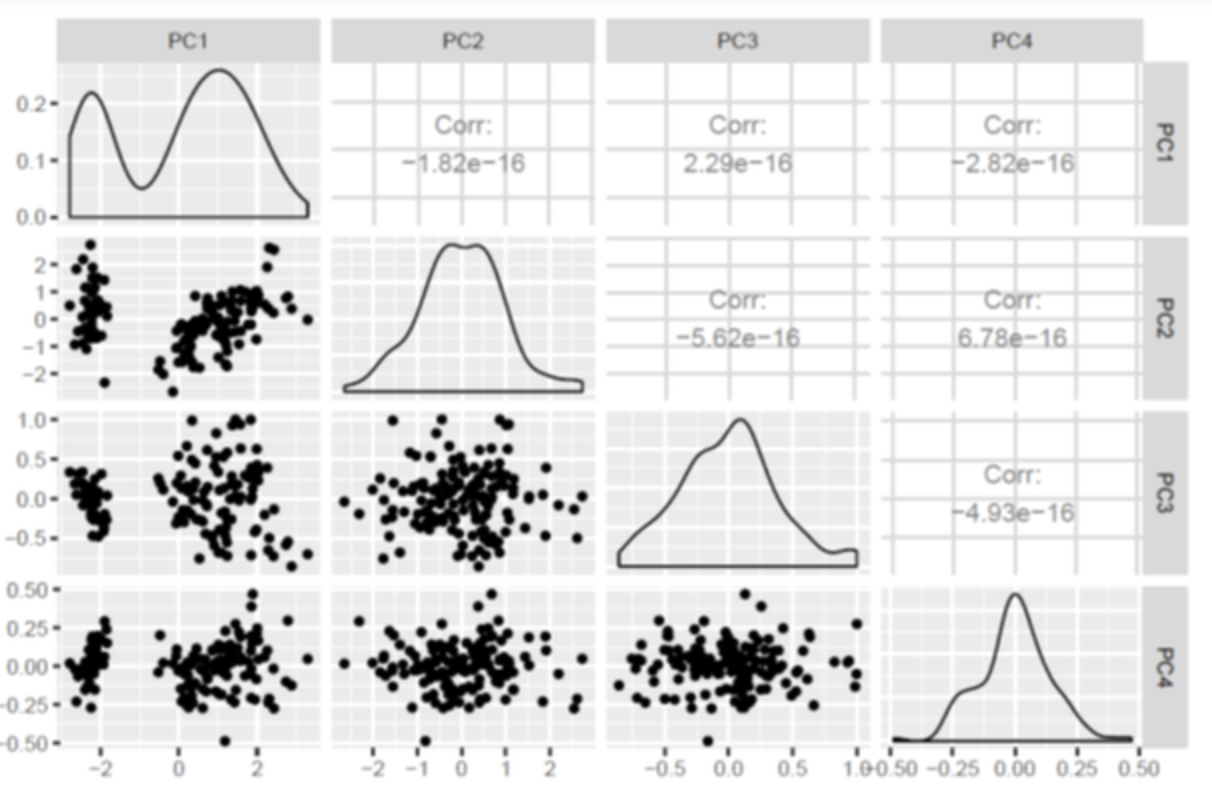
PCA是一种无监督算法,常用于高维、相关数据的特征提取,PCA通过将特征转化为数据集中方差最大的正交分量轴来实现降维。
下图是使用iris数据集实现PCA算法的结果。我们看到,当我们转换到PCA空间时,特征之间的相关性已经被去除。
以下是主成分分析计算得出的有用指标摘要:
 表格中数据显示,PC1、PC2和PC3贡献了99.5%的总方差,因此在最终的机器学习实现中,PC4可以忽略不计。
表格中数据显示,PC1、PC2和PC3贡献了99.5%的总方差,因此在最终的机器学习实现中,PC4可以忽略不计。
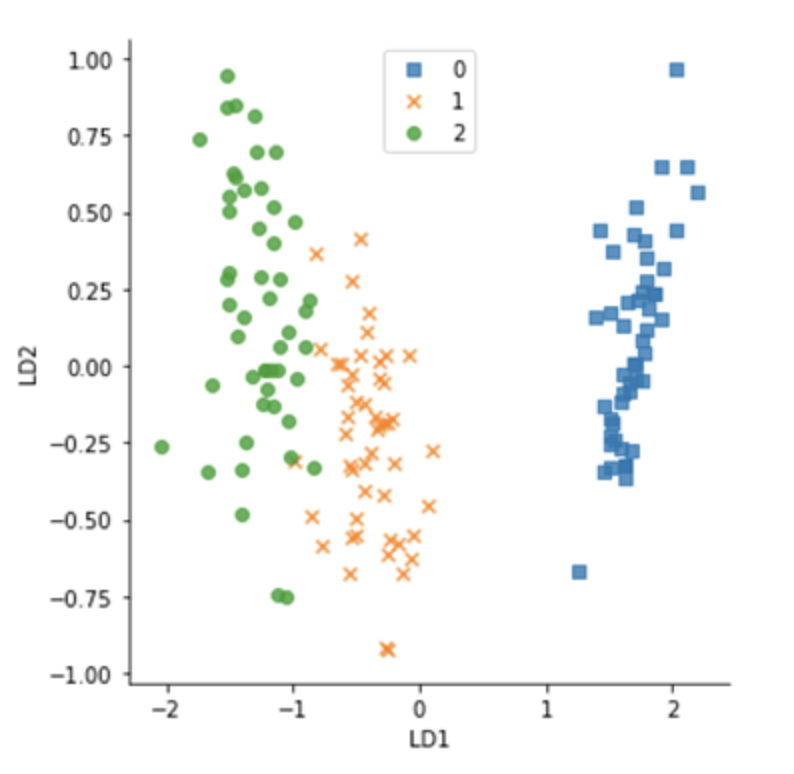
 LDA的目标是找到优化类可分的特征子空间(参见下图)。因此LDA是一种有监督的算法。下图是使用LDA实现的iris数据集的输出。它表明了在LDA空间中鸢尾类的线性可分性。注意,LD1捕获了大多数类的可分辨性。
LDA的目标是找到优化类可分的特征子空间(参见下图)。因此LDA是一种有监督的算法。下图是使用LDA实现的iris数据集的输出。它表明了在LDA空间中鸢尾类的线性可分性。注意,LD1捕获了大多数类的可分辨性。
收藏
 理工酷
理工酷
 资源下载
资源下载