是的,神经网络就是数学函数。最简单的结构是是一个输入节点,一个权重和一个输出节点。
神经网络
当添加多层时,神经网络仍然只是一个函数,只是随着信号从一层到另一层传递,它成为了功能的组合。权重只是函数中的参数,可以对其进行微调以降低损失(通常是通过梯度下降)。
在ML的早期,只有线性分类器,例如线性感知器和线性SVM。这些只能在数据可线性分离时对问题进行分类。这只能表明,如果将输入和输出绘制为网格上的数据点,则可以用一条线分隔两个类。效果如下图所示:
 左边的图像是感知器和线性SVM可以对数据进行准确分类的图像,而右边的图像则不能。
“人工智能”只能学习线性划分,但这并不能解决许多现实问题。
1989年,乔治·西本科(George Cybenko)表明,具有单个隐藏层的神经网络可以在R ^ n的紧子集上任意近似一个连续函数。
在同一时间非线性SVM被开发出来,因此它们也可以用于非线性可分离数据。
这并不意味着神经网络总是比非线性SVM更好,并且在数据集较小的情况下,非线性SVM可以轻松胜过神经网络。
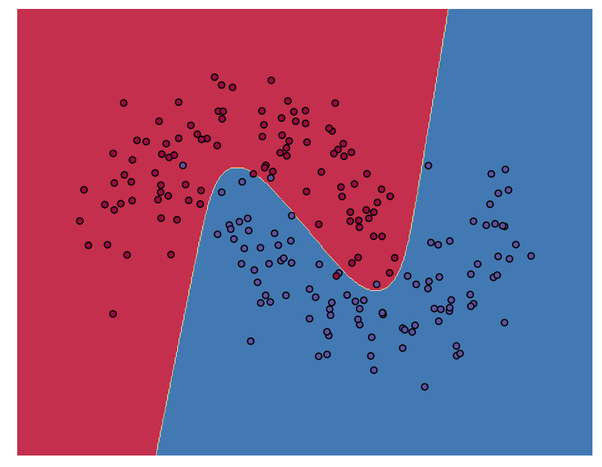
Cybenko的结果表示,浅层网络(和非线性SVM)具有学习任何决策边界(或更高维度的决策面)的能力。因此,不再只有线条,而是任意的曲线和曲面。
这是非线性决策边界(2-D)将绘制的数据点分为两类的可视化表达。
左边的图像是感知器和线性SVM可以对数据进行准确分类的图像,而右边的图像则不能。
“人工智能”只能学习线性划分,但这并不能解决许多现实问题。
1989年,乔治·西本科(George Cybenko)表明,具有单个隐藏层的神经网络可以在R ^ n的紧子集上任意近似一个连续函数。
在同一时间非线性SVM被开发出来,因此它们也可以用于非线性可分离数据。
这并不意味着神经网络总是比非线性SVM更好,并且在数据集较小的情况下,非线性SVM可以轻松胜过神经网络。
Cybenko的结果表示,浅层网络(和非线性SVM)具有学习任何决策边界(或更高维度的决策面)的能力。因此,不再只有线条,而是任意的曲线和曲面。
这是非线性决策边界(2-D)将绘制的数据点分为两类的可视化表达。
深度学习
Cybenko表明可以通过某些神经网络来实现这一目标。但他从来没有讨论过如何学到浅网络(一个隐藏层)的参数。在那之后,人们开始添加神经网络的层数。这就是深度学习产生的方式。 人们对神经网络如何近似任何连续函数感到好奇,但是不确定该如何去做,因此他们增加了更多的层数。通过增加层,可以学习输入数据之间越来越抽象的关系。 严格来说,浅层网络可以学到任何深层网络可以学到的东西,只是没有已知的方法可以使这种方法对ML问题变得切实可行。
注意
是神经网络是通用函数逼近器,但还有其他一些。它们在数学上并不像看起来那样独特。 转载自:https://www.quora.com/Is-neural-network-basically-just-a-function
 理工酷
理工酷
 资源下载
资源下载