理工酷

本质上，对于任何机器学习问题，都可以将数据点分为两个部分：模式+随机噪声。 例如，如果你要为公寓的价格建模，你会知道价格取决于公寓的面积。因此这个因素促成了这种模式：更多的卧室通常会导致更高的价格。但是，具有相同面积的公寓，会随着卧室数量的不同导致价格的不完全相同。其中，价格的变化就是噪音。 再举一个例子，比如考虑开车。给定具有特定曲率的曲线，则存在最佳的转向方向和最佳速度。当你在该曲线上观察到100个驾驶员时，其中大多数将接近最佳转向角和速度。但是它们不会具有完全相同的转向角和速度。同样，道路的曲率会影响转向角和速度的模式，然后会产生噪声，导致偏离该最佳值。 现在机器学习的目标是对模式进行建模并忽略噪声。一个算法除了试图拟合模式外，还试图拟合噪声，这就是过度拟合，而一个算法在试图避免拟合噪声时错过了模式，它就是欠拟合。 过拟合的迹象：样本内误差低，样本外误差高。 拟合不足的迹象：样本内误差高，样本外误差高。

在有监督的设置中，通常希望将预测函数的输出与训练标签相匹配。因此，在上面的驾驶示例中，需要准确预测转向角和速度。随着不断添加越来越多的变量（例如道路的曲率，汽车的模型，驾驶员的经验，天气，驾驶员的情绪等），你将倾向于对训练数据做出越来越好的预测。 然而在一点之外，添加更多的变量也无助于对模式进行建模，而只是试图拟合噪声。由于噪声是随机的，因此不能很好地推广到看不见的数据，因此您的训练误差和测试误差均较小。 请考虑以下情形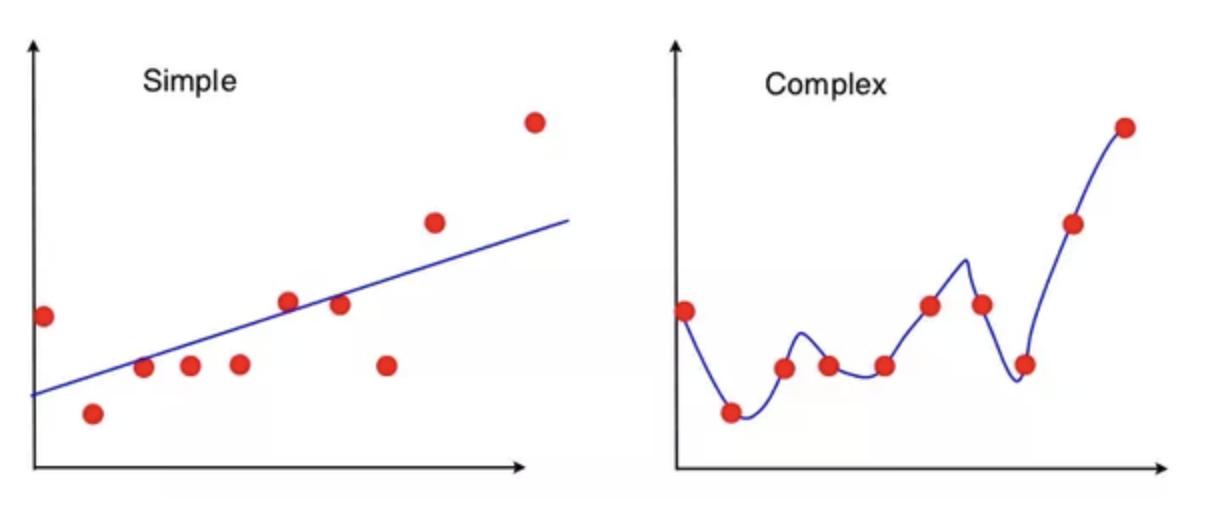： 左边的算法返回给定这些点的最佳拟合线，而右边的算法返回给定的n点的度k的最佳拟合多项式。 （在此示例中，k是一个较大的数字，例如10。） 如果将最低点向上移动一定距离会怎样？ 左图中的线变得稍微平一些，在左侧向上移动一点，在右侧保持大约相同的位置。但是，右侧的曲线变化很大，你在第1点和第3点之间看到的跌落可能会完全消失。 显然，右侧的算法正在拟合噪声。从该示例可以看出，减少过度拟合的方法是人为地惩罚高阶多项式。这确保了只有在与较简单的模型相比可以显着减少误差的情况下，才选择更高阶的多项式来克服惩罚。 你可以创建一个类似的示例来演示欠拟合，可以使用二次函数对模式进行建模的数据。然后，如果使用线性函数作为预测变量来避免拟合噪声，则也将无法很好地拟合模式。