简单的解释
axis(轴)表示多维矩阵的第几维. ndarray.sum(axis=1) 表示取编号为 1 的维上的数据执行聚合函数(这里是求和),得到的结果是把这一维压缩掉的矩阵,而压缩的方法就是这里使用的聚合函数 sum.
详细的解释
axis(轴) 和 索引, 维度(ndim), shape 放在一起就容易理解了.
标量(单个数字)和一维矩阵(向量)好理解,这里不多说了. 这里从二维看起.
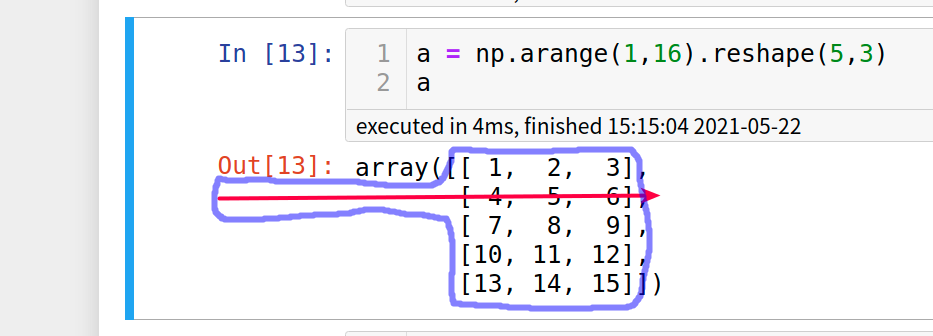
In [2]: a = np.arange(1,13).reshape(3,4)
...: a
Out[2]:
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
In [3]: a[1,2]
Out[3]: 7
In [4]: a.ndim
Out[4]: 2
In [5]: a.shape
Out[5]: (3, 4)
In [6]: a.sum(axis=1)
Out[6]: array([10, 26, 42])
In [7]: a[0,:]
Out[7]: array([1, 2, 3, 4])
In [8]: a[1,:]
Out[8]: array([5, 6, 7, 8])
In [9]: a[2,:]
Out[9]: array([ 9, 10, 11, 12])
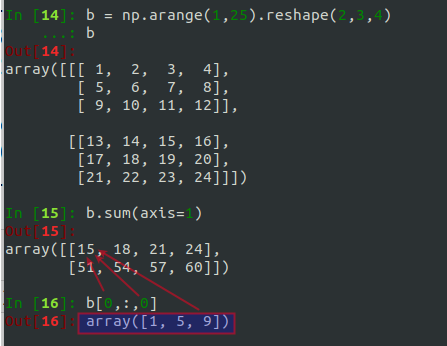
In [14]: b = np.arange(1,25).reshape(2,3,4)
...: b
Out[14]:
array([[[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]],
[[13, 14, 15, 16],
[17, 18, 19, 20],
[21, 22, 23, 24]]])
In [15]: b.sum(axis=1)
Out[15]:
array([[15, 18, 21, 24],
[51, 54, 57, 60]])
In [16]: b[0,:,0]
Out[16]: array([1, 5, 9])
对于二维矩阵 a, a[1,2]表示a的1行2列的元素(从0开始编号). 这里, [1,2]称作对应的那个元素(7)的索引. 中括号里,由逗号(,)分隔的元素最多可以写几个,也就是确定单个数字的位置需要几个数,表示这个矩阵有几个维度(ndim). 每个维度上有几个编号,也就是那个维度上的位置编号不能超过几(严格小于),把它们按顺序都列出来,就是shape了.
在做统计时,想把某个维度上的数据拎出来做个统计,就需要指明是哪个维度,用来指明哪个维度的术语就是axis(轴)了.
我不建议使用图示的方法理解沿轴做统计,因为对于二维三维的矩阵,还勉强可以画出来,但对于更高维的矩阵,这种理解就成为障碍了.下面直接从表示形式上解释这个逻辑.
对于上面的二维矩阵a, a.sum(axis=1)表示 a[保持不动原样输出的维,拎出来做统计的维]的统计结果

对于更高维的矩阵,比如上面的 b, 这个解释扩展起来也非常方便. b.sum(axis=1) 表示 b[保持不动原样输出的维,拎出来做统计的维,保持不动原样输出的维]的统计结果
ps. 歪个楼, 后记
axes是axis的复数形式,也是斧头的复数. 当沿二维矩阵贯穿一个箭头来指明沿哪个方向统计的时候, 画出来的示意图像不像一个斧头?

 理工酷
理工酷
 资源下载
资源下载