介绍几个图像去噪技术
一、空间过滤
分为线性和非线性滤波器。
1.线性滤波器
对高斯和椒盐噪声有效。
(1)均值滤波器
它是一个简单的滑动窗口滤波器,它用内核窗口中所有像素值的平均值替换了内核窗口中的中心像素值。
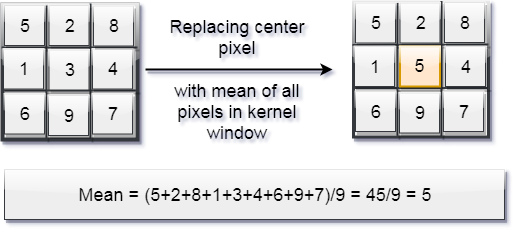
从均方误差的意义上讲,均值滤波器是针对高斯噪声的最佳滤波器。
(2)Weiner滤波器/维纳滤波器
一种统计方法,用于去除信号中的噪声。
先决条件————用户必须了解原始信号和噪声的频谱特性(例如-功率函数)。 目的————为了具有最小的均方误差(MSE),即原始信号和新信号之间的差异应尽可能小。
Assume W(x, y) is a weiner filter,
Restored image will be given as -
Xn(x, y) = W(x, y).Y(x, y)
where,
Y(x, y) is the received image(Degraded).
Xn(x, y) is the restored image.
在减小MSE误差的同时获得的维纳滤波器方程为

其中,
- ||H(x, y)||^2 = H(x, y)H*(x, y);
- H(x, y) =degradation function(退化函数);
- H*(x, y) = complex conjugate of degradation function(退化函数的复共轭);
- Sn(x, y) = ||N(x, y)||^2 即噪声的功率谱;
- Sf(x, y) = ||F(x, y)||^2 即原始图像的功率谱;
注意:仅当基础信号平滑时,Weiner滤波器才能很好地工作。
线性滤波器的缺点: 线性滤波器趋于模糊锐利边缘,破坏线条和其他精细图像细节,并且与信号有关的噪声存在的情况下表现不佳。
2.非线性滤波器
使用非线性滤波器,不需要明确识别噪声就可以消除噪声。
(1)中值滤波器
它是一个简单的滑动窗口滤波器,它将内核窗口中的中心像素值替换为该内核窗口中所有像素值的中值。
注:内核大小必须为正整数。
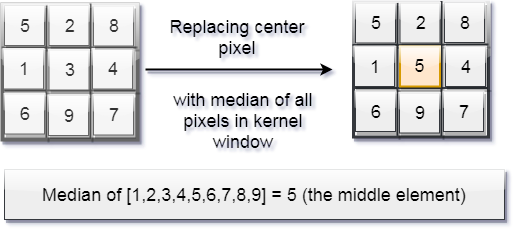
在这里,大小为9,因此 (9+1)/2 = 第5个元素是中位数。
(2)加权中值滤波器
“中值”和“加权中值”过滤器之间的唯一区别是蒙版的存在,此蒙版具有一些权重(或值)并取平均值。
- 该加权掩码乘以内核窗口的像素。
- 像素按升序排列。
- 从排序列表中找到中间值。
- 将此中位数放在中心。

优点:
- 可以保留边缘。
- 在消除脉冲噪声方面非常有效。
- 它们比线性滤波器更强大,因为它们能够在不模糊边缘的情况下降低噪声水平。
二、转换域过滤
可以根据对基本变换函数的选择对变换域滤波方法进行分类,这些基础变换函数包括非数据自适应和数据自适应滤波器。 非数据自适应过滤器比数据自适应过滤器更受欢迎。
1.非数据自适应滤波器
非数据自适应滤波器进一步分为两个域,即空间频率域和小波 领域。
(1)空间频率滤波 空间频率滤波是指使用快速傅立叶变换(FFT)低通滤波器。 在这里,我们预先定义了一个截止频率,该滤波器使所有低于该截止频率的频率通过,并使所有大于该截止频率的频率衰减。
在频域中进行滤波的原因通常是因为,与在图像(空间)域中进行卷积相比,执行2D傅里叶变换和滤波器乘法的计算速度更快。
注:图像(空间域)中的卷积等效于频域中的乘法。
(2)小波域 小波是一种数学函数,用于将给定函数或连续时间信号划分为不同的比例分量。
小波变换是由小波表示的函数。 小波域中的滤波方法进一步分类为:
线性滤波器 当存在基于高斯的噪声且准确度标准为均方误差(MSE)时,Weiner滤波器会产生最佳结果。但是,基于此假设设计滤波器得到的结果往往不理想。
非线性阈值滤波
为什么阈值化可以有效降低噪音?
基于以下假设:
- 小波变换的去相关属性会产生稀疏信号:大多数未触及系数为零或接近零。
- 噪声沿所有系数平均分布。
- 噪声水平不是很高,因此我们可以将信号小波系数与噪声小波系数区分开。
阈值处理有两种类型——硬性和软性。
硬阈值是“保留或杀死”程序,并且直观上更具吸引力。
The hard thresholding operator with threshold t is defined as -
D(U, t) = U for all |U| > t
= 0 otherwise
软阈值将系数的绝对值收缩到阈值以上。
The soft thresholding operator with threshold t is defined as -
D(U, t) = sgn(U)max(0, |U| - t)
软阈值相比硬阈值的优势: 有时,纯噪声系数可能会超过硬阈值,并在输出中显示为令人讨厌的“斑点”。 软限制可以缩小这些错误的结构。
各种阈值过滤技术之间的区别仅在于阈值选择,阈值过滤的基本过程保持不变:
- 计算图像的离散小波变换(DWT)。
- 阈值小波系数(阈值可以是通用的,也可以是子带自适应的)
- 计算逆DWT以获取去噪后的估计值。
2.数据自适应变换
独立成分分析(ICA): “独立成分分析(ICA)是一种从多元(多维)统计数据中查找潜在因素或成分的方法。ICA与其他方法的区别在于,它寻找的是统计上独立且非高斯的成分。”
——A.Hyvarinen,A.Karhunen,E.Oja
假设:非高斯信号。
该假设有助于算法对同时具有非高斯分布和高斯分布的图像进行降噪。
与基于小波的方法相比,缺点是
- 计算成本,因为它使用了滑动窗口。
- 它需要无噪声数据或同一场景的至少两个图像帧的样本。 在某些应用中,可能难以获得无噪声训练数据。
除了所有这些技术之外,还有另一种技术:
- 去噪自动编码器,用于消除图像中的噪声。
参考https://iq.opengenus.org/image-denoising-and-image-processing-techniques/
 理工酷
理工酷
 资源下载
资源下载