理工酷

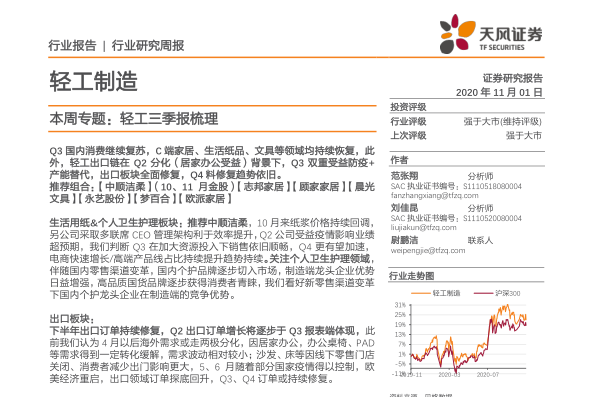
1x1的卷积矩阵本质上压缩了输入体积的深度尺寸(W x H x D)，而宽度和高度保持不变(W x H x1)。相比之下，一个n x n的卷积矩阵不仅可以压缩输入体积的深度尺寸，它还可以根据其尺寸、输入体积尺寸和pad值改变输入体积的宽度和高度。

当我们尝试在二维中可视化1x1卷积时，它看起来像如下所示的矩阵乘法(图1)，即深度为1的输入，6 × 6 × 1乘以1 × 1 × 1得到6 × 6 × 1的输出。在这种情况下值得注意的是，如果我们有两个1 x 1的卷积滤波器，我们的输出将是6 x 6 x 2(深度2)。

但当我们考虑深度大于1的输入体积时，我们可以看到1x1卷积的真正作用如下图所示(图2)。它不再是一个简单的矩阵乘法。

为了简单起见，让我们使用前面图片(图1)中所示的6 x 6矩阵，并多次复制它来创建深度为32的体积。我们对1 x 1矩阵也做同样的事情。现在，位置4,3中的item的值（在图1中为4）将与1x1的值2相乘。

但是由于它具有32层，并且我们复制了相同的矩阵，因此将在绿色点中填充结果值，在图2的右边是值RELU（（2 * 4）* 32），其中RELU是非线性的（请注意，我们将对深度计算的所有值求和）。

下面的图表(图3)说明了这一点。这就好像一个代表1x1卷积的单个神经元计算所有黄色圆圈的加权和，并通过非线性传递结果数字。

所以我们可以用1 x1卷积来改变输入量的深度(通过选择过滤器或多或少比输入量)的深度,以及输入量通过非线性(如果1 x1过滤器的数量保持相同的作为输入量,那么它所做的就是添加一个非线性)。使用1x1卷积来降低深度，除了作为降维操作外，还可以将网络的计算成本降低一个数量级。

总之，1x1的卷积层可以用来：

• 改变输入体积的深度，就像max pooling改变输入体积的高度/宽度一样。非1x1的卷积除了像1x1的卷积一样将输入体积深度扁平化为1之外，还可以像前面提到的那样改变输入体积的宽度和高度。

• 添加一个非线性层。为了只引入非线性，只需添加1x1个卷积滤波器，其计数与输入体积的深度相同。

• 通过降低深度来降低网络中的计算成本。这在inception network中使用。