理工酷

概率图算法

信念传播算法是概率图算法中的一种，概率图算法大致可以分为两类，第一类是精确推断方法，希望能计算出目标变量的边际分布或条件分布的精确值；遗憾的是，一般情形下，此类算法的计算复杂度随着极大团规模的增长呈指数增长，适用范围有限。第二类算法为近似推断算法，希望在较低的时间复杂度下获得原问题的近似解；信念传播算法是比较有代表性的精确推断算法。

信念传播算法

信念传播算法将变量消去法中的求和操作看作是一个消息传递过程，较好的解决了求解多个边际分布时的重复计算问题。具体来说，变量消去法通过求和操作 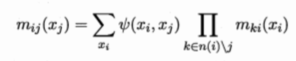消去变量xi其中n(i)表示节点xi的邻接节点。在信念传播算法中，这个操作被看作从xi向xj传递了一个消息mij（xj）。这样变量消去过程就能描述为消息传递过程。不难发现，每次消息传递操作仅与变量xi及其邻接结点直接相关，换言之，消息传递相关的计算被限制在图的局部进行。 在信念传播算法中，一个结点仅在接收到来自其他所有结点的消息之后才能向另一个结点发送消息，且结点的编辑分布正比于它所接收的消息的乘积。 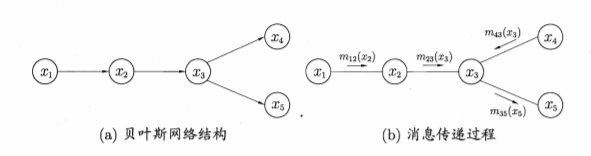例如在上图中，结点x3要向x5发送消息，必须事先收到来自结点x2和x4的消息，且传递到x5的消息m35（x5）恰为概率P（x5） 若图中没有环，则信念传播算法经过两个步骤即可完成所有的消息传递，进而能计算所有变量上的边际分布：

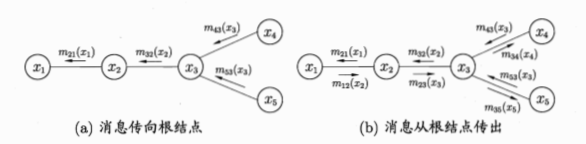
• 指定一个根节点，从所有叶节点开始向根节点传递消息，直到根节点收到所有邻接节点的消息。
• 从根节点开始向叶节点传递消息明知道所有叶节点均收到消息。

例如在上图a中，令x1为根节点，则x4和x5为叶节点，以上两步消息的过程如下图所示，此时图的每条边上都有方向不同的两条消息，基于这些消息和正比关系可获得所有的变量的边际效率。