理工酷

等度量映射

等度量映射的基本出发点是认为低维流形嵌入到高维流形空间之后，直接在高维流形空间中计算直线距离具有误导性，因为高维空间中的直线距离在低维嵌入流形上是不可达的。如下图所示， 低维嵌入流形上两点距离是“测地线”距离：如果想象一只虫子从一点爬到零一点，如果它不能脱离曲面行走，那么下图的红色曲线就是距离最短的路径，即S曲面上的测地线，测地线距离是两点之间的本真距离。显然，直接在高维空间中计算直线距离是不恰当的。 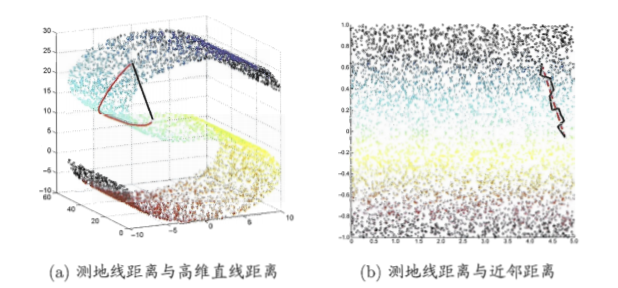那么，该如何计算地线距离呢？这是我们可以利用流形在局部上与欧式空间同胚这个性质，对每个点基于欧氏距离找出其近邻点，然后就能建立一个近邻连线图，图中近邻点之间存在连接，而非近邻点之间不存在连接，于是，计算两点之间测地线距离的问题，就转变为计算近邻连接图上两点之间的最短路径问题。从上图可以看出，基于紧邻距离逼近能够获得低维流形上测地线距离很好的近似。 在近邻连接图上计算两点之间的最短路径，可采用著名的Dijkstra算法或者Floyd算法，在得到任意两点之间的距离之后，就可通过MDS方法来获得样本点在低维空间中的坐标。

注意

Lsomap仅是得到了训练样本在低维空间中的坐标，对于新样本，如何将其映射到低维空间呢？这个问题的常用解决方法，是将训练样本的高维坐标作为输入、低维空间坐标作为输出，训练一个回归学习器来对新样本的低维空间坐标进行预测。