0
神经网络中有一类模型是为网络状态定义一个“能量”,能量最小化时网络达到理想状态,而网络的训练就是在最小化这个能量函数。Boltzmann机就是一种“基于能量的模型”,常见结构如下图所示:
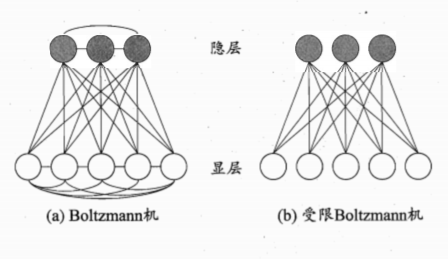
其神经元分为两层:显层与隐层。
显层用于表示数据的输入与输出,隐层被理解为数据的内在表达。
Boltzmann机中的神经元都是布尔型的,只能取0,1两个状态,状态1表示激活,状态0表示抑制。令S表示n个神经元的状态,Wij表示神经元i与j之间的连接权, θi表示神经元i的阈值,则状态向量S对应的Boltzmann机能量定义为:
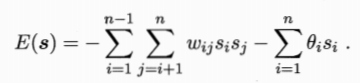 若网络中的神经元以任意不依赖于输入值的顺序进行更新,则网络最终将达到Boltzmann分布,此时状态向量S出现的概率将仅有其能量与所有可能状态向量的能量确定
若网络中的神经元以任意不依赖于输入值的顺序进行更新,则网络最终将达到Boltzmann分布,此时状态向量S出现的概率将仅有其能量与所有可能状态向量的能量确定
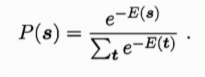
训练过程
Boltzmann机的训练过程就是将每个训练样本视为一个状态向量,使其出现的概率尽可能的大。标准的Boltzmann机是一个全连接图,训练网络的复杂度很高,这使其难以用于解决现实任务。现实中常采用受限Boltzmann机。
受限Boltzmann机
受限Boltzmann机仅保留显层与隐层之间的连接,从而将Boltzmann机结构由完全图简化为二部图。 受限Boltzmann机常用“对比散度”算法进行训练。
收藏
 理工酷
理工酷
 资源下载
资源下载