理工酷

特征选择过程必须保证不丢失重要特征，否则后续学习过程会因为重要信息的确实而无法获得好的性能。给定数据集，若学习任务不同，则相关特征很可能不同，因此，特征选择中的“无关特征”，是指与当前学习任务无关。 有一类特征叫做“冗余特征”，他们所包含的信息能从其他特征中推演出来。例如，若考虑立方体对象，若已有特征“底面长”、“底面宽”则“底面积”是冗余特征。冗余特征在很多时候不起作用，去掉会减轻学习的负担。但有些时候，冗余特征会降低学习任务的难度，例如，学习任务是估算立方体的体积，则“底面积”这个冗余特征的存在将使得体积的估算更加容易；更确切地说，若某个冗余特征恰好对应了完成学习任务所需的“中间概念”，则该冗余特征是有益的。

我们的选择过程主要包含两个阶段

子集搜索

在给定特征集合我们可将每个特征看作一个候选子集，对这d个候选单特征子集进行评价，假定{a_2 }最优，于是将{a_2 }作为第一轮的选定集； 然后，在上一轮选定集中加入一个特征，构成包含两个特征的候选子集，假定这d-1个候选两特征子集中{a_2,a_4 }最优，且优于{a_2 }，于是将{a_2,a_4 }作为本轮的选定集； 假定在k+1轮时，最优的候选（k+1）特征子集不如上一轮的选定集，则停止生成候选子集，并将上一轮选定的k特征集合作为特征选择结果，这样的搜索策略称为前向搜索。 类似的，若我们从完整的特征集合开始，每次去掉一个无关特征，这样逐渐减少特征的策略称为“后向”搜索。还可以将前向与后向结合起来，每一轮逐渐增加选定的相关特征、同时减少无关特征，这样的策略称为“双向”搜索。 上述算法都是贪心的，因为他们仅考虑了使本轮选定集最优

子集评价

还给定数据集D，假定D中第i类样本所占比例为Pi，对于属性子集A，假定根据其取值将D分成了V个子集，每个子集中的样本在A上取值相同，于是我们可计算属性子集的信息增益，信息增益越大，意味着特征子集A所包含的有助于分类的信息越多。于是，对每个候选特征子集，我们可基于训练数据集D来计算其信息增益，以此作为评价准则。 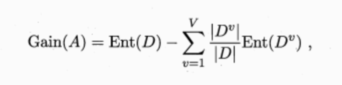更一般的，特征子集A实际上确定了对数据集D的一个划分，每个划分区域对应着A上的一个取值，而样本标记信息Y则对应着对D的真实划分，通过估算这两个划分的差异，这能对A进行评价，信息熵仅是判断这个差异的一个途径其他能判断两个划分差异的机制都能用于特征子集评价。

将特征子集评价搜索机制与子集评价机制相结合，即可得到特征选择方法

例如，前向搜索与信息熵结合，这与决策树算法非常相似。事实上，决策树可以用于特征选择，树节点的划分属性所组成的集合就是选择出的特征子集。其他的特征选择方法未必像决策树特征选择这么明显，但是其在本质上都是显式或者隐式地结合了某钟子集搜索机制和子集评价机制。 常见的特征选择方法大致可以分为三类：过滤式、包裹式、和嵌入式。