1
PCA:
这是一种无监督的方法,用于降维。如果输入空间的尺寸为D,那么理想情况下,你希望选择K <D尺寸,来使K维空间中数据点之间的欧式距离与原始D维空间中的欧式距离非常接近。也就是说,你要尽可能保留数据的差异。
在使用PCA选择K尺寸之前,必须应用仿射变换来使轴去相关。为什么这很重要?
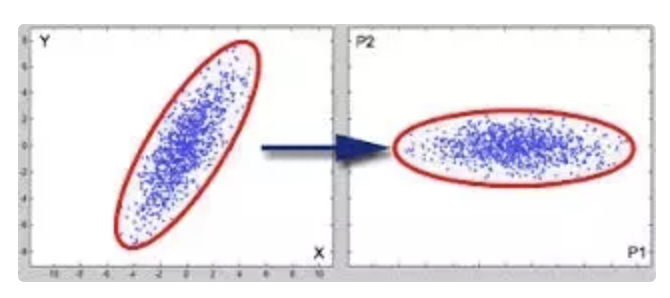
在上面的示例中,你必须从两个维度中选择一个维度,在左图中,选择X或Y轴会导致大量信息丢失(X和Y上的项目数据,并且应该看到它更改分布中的形状和成对距离)。相反,在正确的图像中,我们已将轴对齐为去相关。可以清楚地看到,P2轴的方差很小,因此选择P1时,系统的成对距离或方差存在较小的变化。
总结一下PCA, 1)通过具有零均值并对轴进行解相关来标准化数据。 2)选择具有最大差异量的K个维度。
特征选择:
在上面的示例中,可以说PCA是特征选择的一种手段,因为从本质上讲,你从给定的资源池中挑选出很少的特征。但是,重要的是要注意,这样做的标准是完全不受监督的。你的目的是保留数据的差异,仅此而已。
在特征选择中,你可以定义一个目标,例如数据分类,并且算法将选择导致分类得分增加的维度。为了让大家明白这一点,我们再次看一下用于PCA的图像。
假设我们的任务是自行车分类(哪种类型的自行车?),其中P1与价格信息相关,P2与自行车类型相关。由于不同类型自行车的价格范围相差很大,因此与P2相比,P1的差异很大。使用PCA,你可以为系统选择P1,而作为一种特征选择算法,它可以看到由P1引起的分类任务噪声,并选择P2作为相关特征维数。
收藏
 理工酷
理工酷
 资源下载
资源下载