理工酷

假设最后一个隐藏层用z激活，将softmax函数定义为

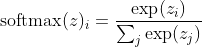
简要解释： softmax函数中的指数几乎可以抵消交叉熵损失中的对数，使得损失z_i近似线性，从而模型错误时可以保持恒定的梯度，使其能够快速进行校正，所以，错误饱和的softmax不会导致梯度消失。

具体一点的解释： 训练神经网络最流行的方法是最大似然估计，以最大化训练数据（大小为m）概率的方式估算参数theta。因为整个训练集的似然度是所有样本的似然度的乘积，所以更容易最大化数据集的对数似然，从而使每个样本的对数似然之和由k表示：

则已知z的softmax函数可替换为

其中，i是第k个样本的正确类别。此时若采用softmax函数的对数来计算样本的对数似然，可得：

上式中对z的较大差值可以大致近似为

首先，可以看到线性分量z_i；其次，可以检查两种情况下max（z）：

1. 如果模型正确，max（z）则为z_i。所以，对数似然趋于零（即似然为1），z_i与z中的其他项之间的差越来越大。

2. 如果模型不正确，max（z）则为z_j>z_i。因此，z_i的添加不能完全抵消-z_j，对数似然近似为（z_i—z_j）。这也清楚地告诉模型如何增加对数似然性：增加z_i和减小z_j。

可以看到，整体对数似然率将由模型不正确的样本决定。同样，即使模型不正确的，导致softmax饱和，损失函数也不会饱和。 z_j近似线性，这意味着我们具有大致恒定的梯度，可以使模型快速进行校正。需要注意注意，均方误差不是这种情况。

可以参考https://www.deeplearningbook.org/