理工酷

简单来说，这两个领域都为另一个极其重要的问题提供了解决方案。（顺便说一句，大部分都是从一个ML人的角度写给其他ML人的。）

机器学习对信号处理的影响

一代人以前，信号处理的中心问题是我们如何分析信号-也就是说，如何从细粒度信号中提取信息，通常是通过将其分解为粗粒度得多的信息来实现。教科书示例将原始音频信号分解为语音，这仍然是该理论的重要应用。

尽管该理论很有用，但对该领域的关注并不完全有益。有时会变得一发不可收拾，就像人们四处走走时声称小波（当时是信号分析文献的重要组成部分）可以用于解决债务危机到制作更好的麦芽威士忌等一切事情一样。有点荒谬的说法。

这个领域所需要的是一个很好的对立面，在1980年代后期，他们通过像Albert Benveniste这样的人得到了它。他和他的小组对了解我们如何就小波实际上擅长于哪些任务的原则提出主张感兴趣。他们有点朝相反的方向：

我们应该对信号建模，而不是对其进行分析。即，我们应该将粗粒度信号视为一组潜在变量，而不是将细粒度信号分解为粗粒度信号，然后使用细粒度信号进行统计推断。这称为多分辨率模型，因为它处理许多分辨率的数据。

将细粒度的观测值拼凑在一起以推断潜在的粗粒度变量的问题（称为合成），比分析要复杂得多。另外，小波合成可以被认为是小波分析的“对立面”。 他们对此领域的贡献之一是将小波合成的任务定位为分层建模问题。可能看起来像下面的树一样模糊，其中细粒度的观察值位于底部，而粗略的潜在变量位于顶部。 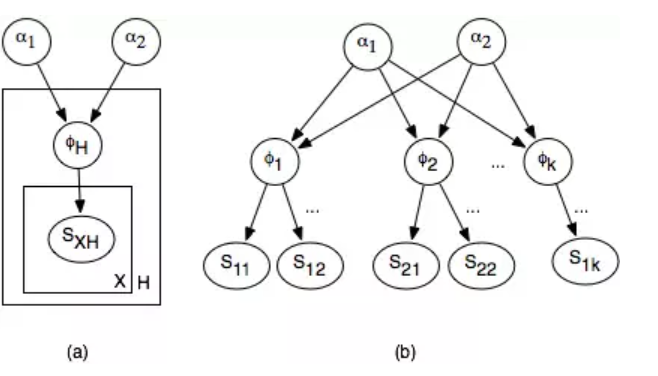现在，如果你了解机器学习，那么你会感到熟悉。这是一个经典的统计推断问题。但这并不是说他们没有自己的问题。

例如，这种信号处理问题在某种程度上是与众不同的，因为它们可能非常庞大，就像当他们试图估计海平面（在地球上的不同点处不同）时一样。“完全庞大”的意思是“ ML人在进行推理时往往会想到的更多潜在变量”。

像Benveniste这样的人似乎很高兴的一点是，信号处理已经从单纯的分析中摆脱出来，转而采用ML的建模机制，并因此受益匪浅。当然，分析仍然是信号处理的一部分，但在很多情况下，ML和信号处理的结合使信号处理器能够解决一些其他领域都无法真正处理的困难推理问题，特别是在信号处理比CS有更重要历史的领域，就像海洋学。

信号处理对ML的影响

过去十年左右的时间，机器学习的标志之一是极高维模型的大量扩散，但总的来说，它不能依赖于用于训练模型的大量数据。如果你是受过经典训练的ML人士，那么你就会知道这是一个严重的问题，如我所画的这张照片所示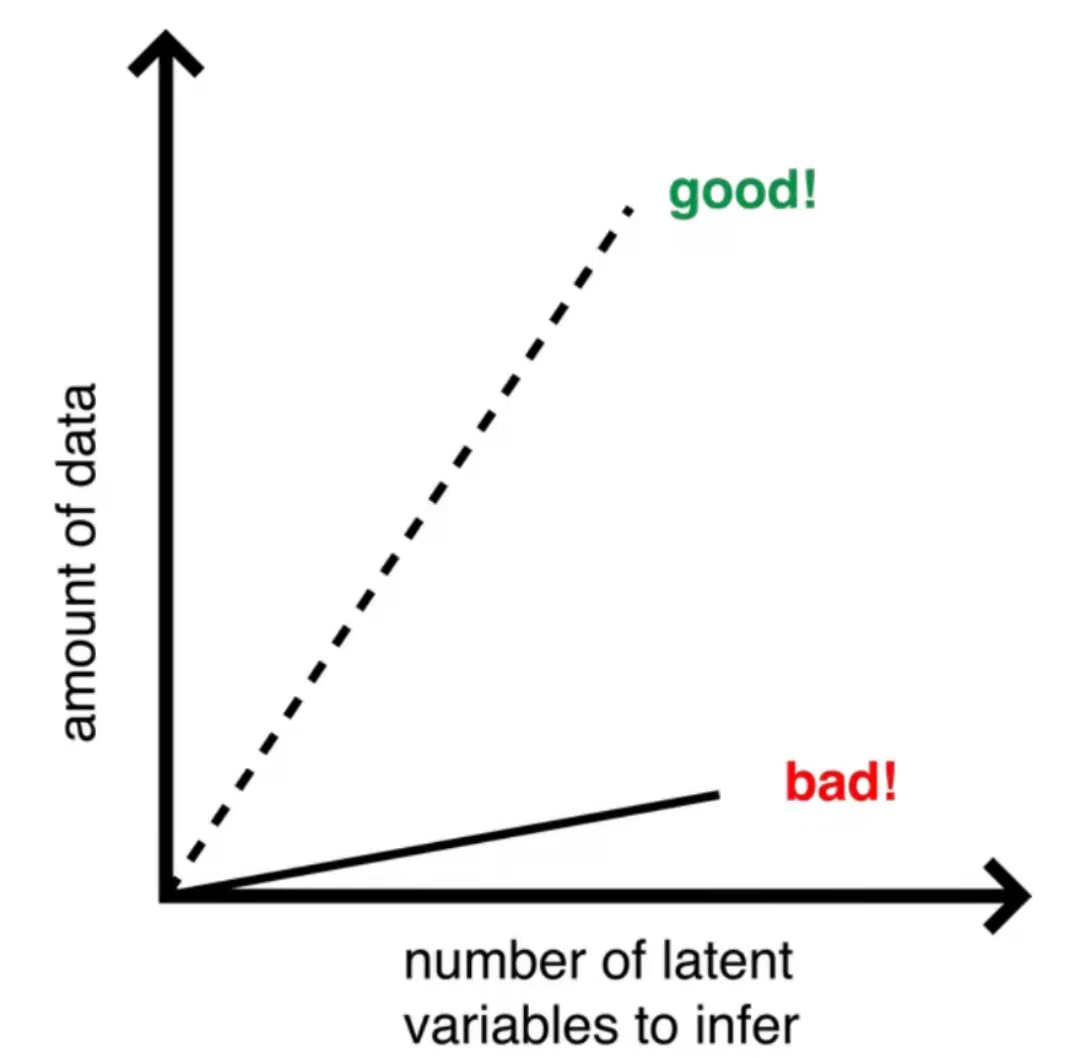： 以非常流行的模型Latent Dirichlet分配为例。它的功能是非常高维的计数数据，在一般情况下，我们希望有很多数据要训练。对于大多数高维模型，如果我们的数据太少，我们最终会遇到非常严重的问题，例如过度拟合。因此，顶线代表我们的总体愿望，底线代表现实。

幸运的是，（对于LDA尤其如此）我们不在乎一般情况。我们通过假设数据（通常也是模型）稀疏来避免此问题，也就是说，我们的大多数功能很少出现，或者对模型不重要。

在过去的十年中，（稀疏地）研究稀疏度如何影响数据的研究。特别是在ML中，这种稀疏的设置导致了嘈杂的矩阵分解方面的突破和矩阵完成（这是Netflix预测奖的实质），以及降维，以及Venkat Chandrasekaren尝试形式化样本复杂度和计算复杂度之间的权衡。这是许多许多其他应用程序中的一些结果。陶仁（Terence Tao），伊曼纽尔·坎德斯（EmmanuelCandès），大卫·多诺（David Donoho）等人还提供了许多其他令人惊奇的非机器学习结果。

总结：实际上，信号处理并不是真正取得这些突破的领域，但是它们所闻名的许多工具和概念都是负责任的（特别是与控制理论风格的数值线性代数结合使用），并且说信号处理人员比ML人更了解稀疏信号似乎并不夸张。

机器学习的许多内容都是关于理解我们如何以及何时进行推理的，而稀疏性方面的文献似乎使我们朝着一个有趣的方向迈进，以真正理解这一问题的存在。无论我们是否喜欢，这种对推理的贡献将在未来十年甚至在未来几十年极大地产生影响。